数据结构与算法—

堆(heap)

堆是一种常用的数据结构，其有两种性质：1.堆中某个节点的值总是不大于或不小于其父节点的值、2.堆总是一棵完全二叉树。堆有多种用法，类似于实现优先队列、堆排序、找最值等等，根据排序方式，堆又分为两种：最小堆(小根堆)、最大堆(大根堆)。最小堆，父节点的值不大于每一个子节点的值，同理可以推出最大堆，就是父节点都不小于每一个子节点的值。

注：这里并不详细介绍堆的二叉树结构，树结构的相关基础知识有必要提前了解一下。

堆排序

堆排序在TopK问题中是最常用的解题方法，堆排序是不稳定的，时间复杂度为$O(n\log n)$，这里来分析一下堆排序，以最小堆/小根堆为例，假设我们给定一个nums数组[]int{0,15,6,10,8,4,9,3,12,7}，我们将这个数组以二叉树的结构表示出来，如下图：

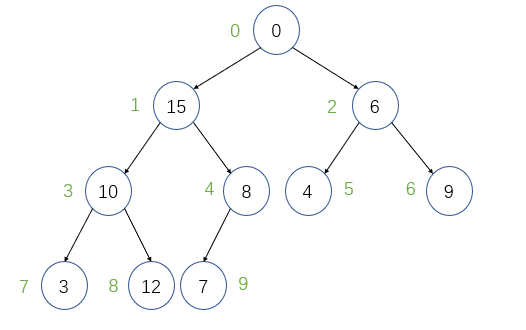
黑色代表的数组中的值，绿色代表的是索引

堆排序的思想是从最后一个父节点开始，通过比较来更新父节点的值，然后在向下沉，即向下更新，我们可以知道父节点的索引为i，子节点的索引为2i+1和2i+2。最后一个父节点的索引为len(nums)/2-1。这里先放出下沉规则的代码，大家跟着代码来理解一下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


func sink(nums []int, n int, i int) {
	//n为数组长度，i为当前父节点的索引
    max := i
    l, r := 2*i+1, 2*i+2
    //如果碰到子节点的值大于父节点，用子节点在中最大的值来替换
    if l < n && nums[l] > nums[max] {
        max = l
    }
    if r < n && nums[r] > nums[max] {
        max = r
    }
    //把父节点换下去并向下调整
    if max != i {
        nums[max], nums[i] = nums[i], nums[max]
        sink(nums, n, max)
    }
}

接下来跟着图来走一遍下沉的思路，首先比较的是最后一个父节点，索引为4，子节点小于父节点的值，不需要更新。然后比较索引3，更换12和10的值，如图：

更换索引3和索引8的值

这里要注意，由于此处更换了父节点，所以要想下沉，自上而下对堆进行排序，要对索引8的子节点进行下沉操作，但是这里8处没有子节点了，所以无需向下沉。然后开始比较索引2，更换6和9的值，如图：

更换索引2和索引6的值

同样需要看一下是否需要向下沉，这里也不需要，接下来比较一下索引1的节点，索引1的节点父节点值都大于子节点，所以不需要替换。然后是索引0的节点，更换0和15的值，如图：

更换索引0和索引1的值

判断一下是否需要继续向下沉，发现对于父节点索引1需要重新进行下沉规则，更换0和12的值，如图：

更换索引1和索引3的值

更换值后，父节点索引为3同样需要继续下沉，再次更换0和10的值，如图：

更换索引3和索引8的值

此时，我们的已经创建好了堆，满足堆的属性，父节点都不小于子节点，而且堆的根节点是最大值。然后接下来要进行的是排序，把第一个值和最后一个值进行更换，这样子最大值就跑到了最后，最后一个值的顺序也就确定，再对前面的值进行上述操作，重新构建堆，如图：

更换第一个值和最后一个值

再次进行上述的下沉规则，这时，最后应该把12和0进行位置更换，最后一个值为12，这样子12也是排序好了，然后再对之前的数进行上述操作，如图：

重新构建堆

更换12和0，12也排序完成，对之前的数再次构建堆。

更换第一个值和最后一个值

以此类推，我们最后就修改了原数组的顺序，结果返回为[]int{0,3,4,6,7,8,9,10,12,15}，这就是最小堆的堆排序，最后的根节点为最小值，所以也叫小根堆。下面是以最小堆为例的完整代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


func heapsort(nums []int, n int) {
	//创建堆，保证父节点和子节点之间的大小关系，遍历父节点
	for i := n/2 - 1; i >= 0; i-- {
		//创建过程中从最后一个父节点开始，向下沉
		sink(nums, n, i)
	}
	//对堆进行排序，将第一个与最后一个值互换，省略对最后一个值的排序
	for i := n - 1; i > 0; i-- {
		nums[0], nums[i] = nums[i], nums[0]
		//排序过程从第一个开始，向下沉
		sink(nums, i, 0)
	}
}

func sink(nums []int, n int, i int) {
	max := i
	l, r := 2*i+1, 2*i+2
	//如果碰到子节点的值大于父节点，用子节点在中最大的值来替换
	if l < n && nums[l] > nums[max] {
		max = l
	}
	if r < n && nums[r] > nums[max] {
		max = r
	}
	//把父节点换下去并向下调整
	if max != i {
		nums[max], nums[i] = nums[i], nums[max]
		sink(nums, n, max)
	}
}

go语言实现堆结构

go语言当中也有封装好的heap包可以使用，不过结构还是要自己来设定，以上面的数组为例，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


func main() {
	nums := []int{0, 15, 6, 10, 8, 4, 9, 3, 12, 7}
	test := &h{}
	heap.Init(test)
	for _, v := range nums {
		heap.Push(test, v)
	}
	//打印堆顶的元素
	fmt.Println((*test)[0])
	//Output: 0

	for test.Len() > 0 {
		fmt.Printf("%d ", heap.Pop(test))
	}
	//Output: 0 3 4 6 7 8 9 10 12 15
}

type h []int

func (h *h) Len() int           { return len(*h) }
func (h *h) Less(i, j int) bool { return (*h)[i] < (*h)[j] }
func (h *h) Swap(i, j int)      { (*h)[i], (*h)[j] = (*h)[j], (*h)[i] }

func (h *h) Push(v interface{}) {
	*h = append(*h, v.(int))
}

func (h *h) Pop() interface{} {
	old := *h
	n := len(old)
	v := old[n-1]
	*h = old[0 : n-1]
	return v
}

这里面应用到的就是container/heap这个包，go语言只是封装了一个堆，其他的需要定义的都由开发者自己去设定。可以点击进去查看一下这个heap包，其中有两个文件，example_intheap_test.go和example_pq_test.go，这两个文件就是堆和优先队列，官方给的例子文档，仿照这个来写就可以，这里解释一下。

首先看一下上述例子或者example_intheap_test.go中的代码，Len()和Swap()这两个函数很好理解，一个是返回数组的长度，一个是交换值，Less()函数这里是决定创建的堆是最小堆还是最大堆，即返回结果为真的顺序，上述例子中return h[i] < h[j]，即返回的是从小到大，也就是最小堆。而Pop()和Push()两个函数，分别是出堆顶元素和放进堆里元素，每次Pop()和Push()后，堆都会自动更新顺序，这也就是go语言为我们实现的。

那么有的人就疑惑了，这还要写这么多为什么不封装好呢？这里就是第二个例子，也就是example_pq_test.go中的优先队列，可以是用普通的线性结构来创造优先队列，但这里使用堆来创造会更简单。下面再举一个优先队列的例子，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57


func main() {
	//要添加进队列的学生名单
	list := []Student{
		{"James", 18},
		{"Karsa", 16},
		{"Bob", 19},
	}
	//已存在队列中的学生名单
	pq := &PQ{
		{"David", 20},
	}
	heap.Init(pq)
	for _, v := range list {
		heap.Push(pq, v)
	}
	fmt.Println((*pq)[0])
	//Output: {Karsa 16}
	for pq.Len() > 0 {
		fmt.Println(heap.Pop(pq))
	}
	//Output: {Karsa 16}
	//        {James 18}
	//        {Bob 19}
	//        {David 20}
}

type Student struct {
	Name string
	Age  int
}

type PQ []Student

func (pq *PQ) Len() int {
	return len(*pq)
}

//以年龄大小排序
func (pq *PQ) Less(i, j int) bool {
	return (*pq)[i].Age < (*pq)[j].Age
}

func (pq *PQ) Swap(i, j int) {
	(*pq)[i], (*pq)[j] = (*pq)[j], (*pq)[i]
}

func (pq *PQ) Push(v interface{}) {
	*pq = append(*pq, v.(Student))
}

func (pq *PQ) Pop() interface{} {
	n := len(*pq)
	v := (*pq)[n-1]
	*pq = (*pq)[:n-1]
	return v
}

上面这就是简易的优先队列的实现，其实相对于堆的数组就是用结构体中的某一个值来充当比较大小的值。另外，在example_pq_test.go代码中有个新的update()，顾名思义是用来修改优先队列中表示优先级的值的，需要额外给结构体添加一个表示索引的字段。

接下来我们看一下利用堆结构来做的算法题：

LeetCode 347. 前 K 个高频元素

给你一个整数数组nums和一个整数K，请你返回其中出现频率前K高的元素。你可以按任意顺序返回答案。

这道题就很容易能想到用堆结构，结构体中带上数组中值和值出现的次数就可以，在Less()函数中用值出现的次数来做比较。然后最后出堆顶K次即可，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49


func topKFrequent(nums []int, k int) []int {
	maps := make(map[int]int)
	for i := 0; i < len(nums); i++ {
		if _, ok := maps[nums[i]]; ok {
			maps[nums[i]]++
		} else {
			maps[nums[i]] = 1
		}
	}

	iheap := &Iheap{}
	heap.Init(iheap)

	for key, value := range maps {
		if iheap.Len() < k {
			heap.Push(iheap, [2]int{key, value})
		} else {
			if (*iheap)[0][1] < value {
				heap.Pop(iheap)
				heap.Push(iheap, [2]int{key, value})
			}
		}
	}

	res := make([]int, k)
	for i := 0; i < k; i++ {
		res[k-i-1] = heap.Pop(iheap).([2]int)[0]
	}

	return res
}

type Iheap [][2]int

func (h Iheap) Len() int           { return len(h) }
func (h Iheap) Less(i, j int) bool { return h[i][1] < h[j][1] }
func (h Iheap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *Iheap) Push(x interface{}) {
	*h = append(*h, x.([2]int))
}

func (h *Iheap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}

LeetCode 264. 丑数 II

给你一个整数n，请你找出并返回第n个丑数。丑数就是只包含质因数2、3和或5的正整数。

首先先了解题意的丑数是什么意思，题干说了因数只包含2、3、5的正整数，所以其实就是2、3、5三个数互相乘积计算得到的数，并继续互相乘积，最后计算得到的就是丑数，比如如果x是丑数，那么2x、3x、5x也都是丑数。这道题也完全可以是用堆来做，用最小堆，首先将1加入堆中，1通常被视为丑数。每次堆顶都会是最小值，把乘法计数的值都存进堆中，需要一个hash来判断是否已经存过，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51


type Heap []int

func (h *Heap) Len() int {
    return len(*h)
}

func (h *Heap) Less(i, j int) bool {
    return (*h)[i] < (*h)[j]
}

func (h *Heap) Swap(i, j int) {
    (*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}

func (h *Heap) Push(v interface{}) {
    *h = append(*h, v.(int))
}

func (h *Heap) Pop() interface{} {
    v := (*h)[len(*h)-1]
    *h = (*h)[:len(*h)-1]
    return v
}

func nthUglyNumber(n int) int {
    var res int
    box := make(map[int]bool)
    var h Heap
    heap.Init(&h)

    
    heap.Push(&h, 1)
    for n > 0 {
        res = heap.Pop(&h).(int)
        fmt.Println(res)
        if !box[res*2] {
            box[res*2] = true
            heap.Push(&h, res*2)
        }
        if !box[res*3] {
            box[res*3] = true
            heap.Push(&h, res*3)
        }
        if !box[res*5] {
            box[res*5] = true
            heap.Push(&h, res*5)
        }
        n--
    }
    return res
}